なぜかけ算の順序を決めて指導するのか

　しばしばネットで「かけ算の問題で、式のかける数とかけられる数を反対に書いたら×にされた」ことが話題になります。

• 「順番を反対にすると意味が変わってくるので間違い」
• 「かけられる数とかける数を反対にしても答えは変わらないので×はおかしい」

　学習指導要領では、算数科の解説編で「10 × 4は、10が4つあることから、40になる」としていますが、順序については規定していません。

　しかし、小学校の算数の教科書は全て順序を定められて書かれています。

　それはどうしてなのでしょうか。

　学校では「教科書では」順序を決めて教えている理由を、指導者の視点から、解説していきます。

※この記事は、かけ算の順序を決めて指導している理由を説明しているものです。指導の是非を論じているわけではないことをご理解ください。

1年生から6年生までの、学習の系統

　算数と数学の違いですが、数学は法則に基づいて抽象的に考えることに対し、算数は

• 具体的な場面を考える
  
• 系統的な積み重ねを大切にする

ことを大切にします。つまり、1年生から6年生まで、同じ原理で積み重ねて行かないと、指導の一貫性が崩れてしまい、教えにくくなるのです。

かけ算の場合

1年生　たし算を学ぶ

2年生　たしざんの繰り返しがかけ算(2＋2＋2＋2 ＝2×4)、九九

3年生　九九より大きな数のかけ算、筆算の方法、倍の計算、交換法則

4年生　小数のかけ算(小数×整数)、分配法則、結合法則

5年生　小数のかけ算(小数×小数)、割合、速さ

6年生　分数のかけ算、比

という系統で学習します。以前の学習が理解している前提で次の学習に進むので、同様のルール(法則)で学ぶことが大切です。

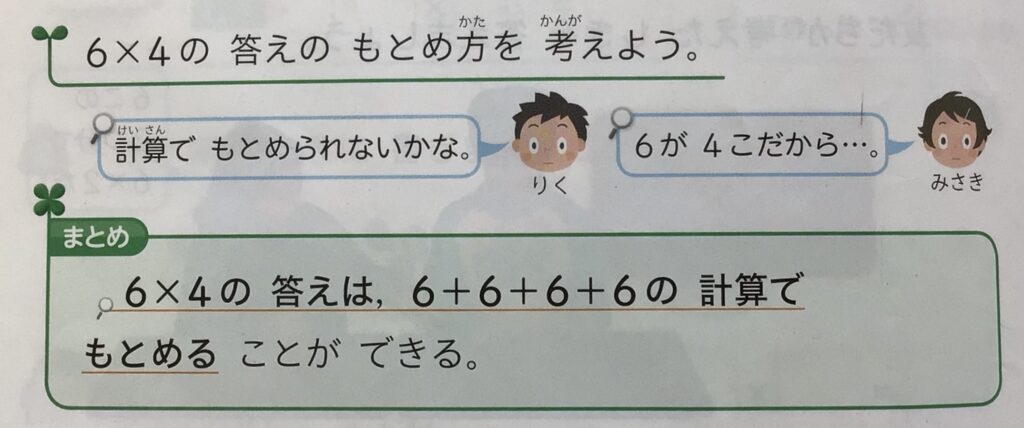
　ポイントとなるのは、2年生で「同じ数のたし算がかけ算」と学習することです。つまり

6を4回たす、6＋6＋6＋6を6×4と表す

と学ぶので、その考えと同じ法則で今後も学ぶことが必要になるのです。

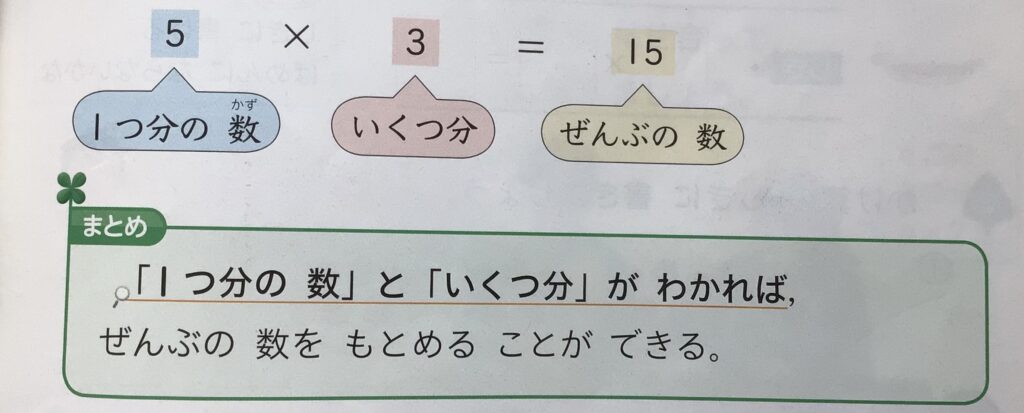
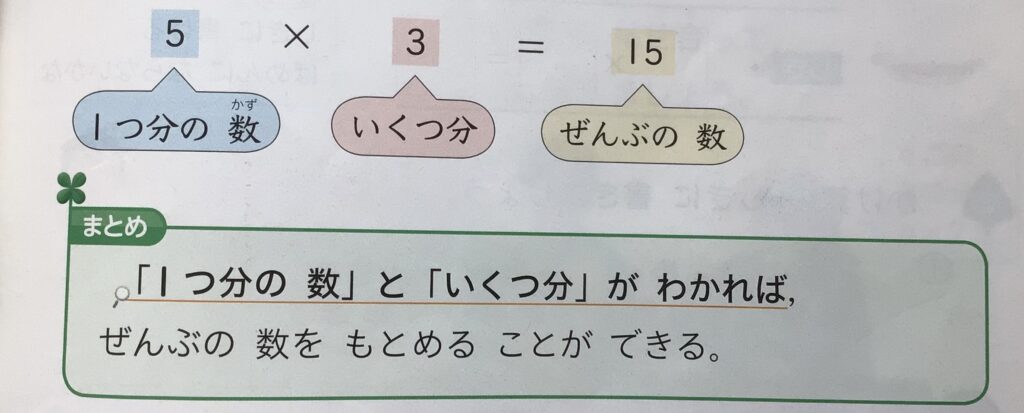
　そして、かけられる数(被乗数)とかける数(乗数)の関係を

1つ分の数(単位量)×いくつ分(倍)＝全部の数(量)

と学習し、おはじきやアレイ図で表します。

3年生以上になると、このことをテープ図を数直線図などで表します。

5年生になると、割合や速度を学習します。

くらべられる量÷もとにする量＝割合
距離÷時間＝速さ

という公式を覚えている方も多いと思いますが、その根拠は

もとにする量×割合＝くらべられる量　(単位量×倍＝求める量)

速さ×時間＝距離　(単位時間あたりの距離×時間＝全体の距離)

だからです。公式だけ覚えても理解したとは言えません。
2年生の頃から学習している「かけ算の決まり」は数値や状況が変わっても変わらないから、系統的に指導ができるのです。

言葉の意味

A×Bの場合

Aは、かけられる数(被乗数)

Bは、かける数(乗数)

です。

順番が逆になったら意味が変わる、と指導しています。

　　　1つの箱にドーナツが3つ入っています。
　　　その箱が5つあります。
　　　ドーナツは何個あるでしょうか。

という問題の場合、式は3×5になります。
被乗数と乗数を反対にして(交換法則)に5×3しても答えは15こで変わりませんが、
「5×3だと、1箱に5こ入っていて、3箱という意味だよ」と指導します。

3X5の場合、乗数と被乗数の関係は

5は3にかける

3は5にかけられる

ことになります。

「かけられる数」と「かける数」を反対にしたら、つまり「○○る」と「○○られる」を反対にしたら意味が変わるのは、次の例を見れば分かるでしょう

この絵を描いて説明するのですが、この絵は

①　人が肉を食べる
②　肉が人を食べる
③　肉を食べる、人が

のどれでしょう。

もちろん①の「人が肉を食べる」です。

つまり、肉は「食べられる」人は「食べる」です。

もし、「「○○る」と「○○られる」を逆に捉えてしまうと

②肉が人を食べる

になってしまいます。

肉は「食べる」人は「食べられる」になってしまうので、そのことを言うと子どもたちは

と叫びます。

①と③は、言葉の順番は違いますが、同じ意味です。
しかし、単純に「数字の順番にかける」と覚えている子どもは
かける数×かけられる数　にしてしまいます。

子どもたちは

• 先に書かれている数をかけられる数にする
• 大きい数から小さい数を割る
• かけ算の答えは大きくなる
• わり算の答えは小さくなる

ととらえがちです。

「計算の順番には意味がある」「問題の状況と言葉の意味を考える」ためにも、「かけられる数」と「かける数」の違いと順序の意味について知っておくと、理解が確実になるのです。

算数と数学の関係

円周を求める公式を、小学校では、直径×円周率(半径×2×円周率)
と学ぶのに対し、中学校では、2πｒ(2×円周率×半径)と学びます。

計算の順番が違います。

小学校の場合、「単位量×倍＝求める数」という法則に基づいて公式にしているのに対し、
中学校は、「乗法の式は、定数を先に、変数を後に書く」という決まりに基づいているからです。

仮に「数学では2πｒなのだから、小学校もこの順番で計算すべきだ」ということになったら、今までの指導の系統から外れてしまうので、子どもは混乱してしまうでしょう。

もちろん、「交換法則を利用した方が楽に計算できる」ときは、それを利用することは「計算のくふう」として推奨されています。

算数は「生活をイメージして考える」ので、

• 系統的に学習する
  
• 言葉の状況を理解して、生活に当てはめて考える
  
• 工夫して、楽に計算する

ことを大切にして指導しているのです。

※2021年11月に実際の授業に即して内容を一部変更しました。